INTRODUCERE

 

 

Metoda lui NEWTON sau metoda tangentei este în prezent una din puţinele metode aplicate în practică pentru rezolvarea ecuaţiilor neliniare.

Cu ajutorul teoremei lui Kantorovici se poate trage concluzia privind unicitatea, existenţa şi domeniul în care se găseşte soluţia.

 

1.Scurt istoric

Încă din antichitate ecuaţiile au avut un rol important în matematică.

În Mesopotamia antică era cunoscută formula de rezolvare a ecuaţiei de gradul al doilea , cu coeficienţii a, b pozitivi, ecuaţie echivalentă cu sistemul de gradul al doilea:

, 

a cărui rezolvare o reduceau la o extragere de rădăcină pătrată punând:

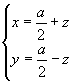, de unde  

.

Ceea ce am scris algebric era exprimat în cuvinte. Textele păstrate conţin şi probleme a căror transpunere se exprimă acum printr-un sistem de ecuaţii, care împlică operaţii de forma:

 cu coeficienţi numere întregi.

Întâlnim şi probleme numerice care conduc la rezolvarea ecuaţiilor de gradul 4, 6 sau 8, reductibile la gradul al doilea.

Diofant (sec. III- IV) rezolva şi sistemele de forma:

 reţinând numai soluţiile pozitive, ca şi sistemele de forma: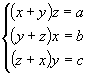 

etc.

În vechiul Babilon erau cunoscute câteva cazuri simple de triunghiuri dreptunghice cu laturile numere naturale, de exemplu: 3, 4, 5; 5, 12, 13; 7, 24, 25; 8, 15, 17 etc., dar problema generală a rezolvării în numere întregi a ecuaţiei pitagorice:  a fost pusă în chiar şcoala lui Pitagora (sec. VI î.e.n.), unde era cunoscută o soluţie în numere prime între ele:

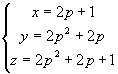
Diofant rezolva în numere întregi ecuaţii de felul  numite ecuatii diofantice. Rezolvarea se referea la valori numerice particulare ale coeficienţilor; dar soluţia era obţinută prin raţionamente aritmetice, nu prin încercari. Diofant determina o singură soluţie pozitivă.

În Evul Mediu rezolvarea ecuaţiilor de gradul întâi şi al doilea nu prezenta dificultăţi.

Magavira (sec. IX) considera ecuaţii reductibile la gradul al doilea, de forma:

.

Al Kasi (sec. XIV - XV) a dat o metodă de rezolvare prin aproximaţii a ecuaţiei particulare   printr-un procedeu de iterare. Metodele de rezolvare numerică ale lui Al Kasi sunt printre cele mai importante rezultate ale ştiinţei arabe.

Până în secolul al XVII-lea n-au fost obţinute metode de rezolvare a ecuaţiilor de grad oarecare şi pe de altă parte, chiar pentru ecuaţiile de gradul al treilea şi al patrulea formulele cunoscute sunt prea complicate, deci nepractice. Numeroasele probleme de geometrie, de astronomie necesită determinarea unei soluţii reale într-un interval dat. Astfel au fost căutate formule de rezolvare prin aproximări a ecuaţiilor numerice.

Simon Stevin a observat ca un polinom f(x) (o funcţie continuă), pentru care f(a)*f(b)<0 are o rădăcina în intervalul (a,b). Micşorând intervalul, prin calcule succesive, putem să ne apropiem de rădăcină.

Rene Descartes a arătat ca numărul de rădăcini pozitive ale unei ecuaţii algebrice este cel mult egal cu numărul variaţiilor şi diferă de acesta printr-un număr par. Făcând transformarea x® -x obţinem o limitare şi a numărului rădăcinilor negative, deci în total, a rădăcinilor reale ale ecuaţiei.

Isaac Newton a dat, în 1707, o metodă pentru determinarea marginilor rădăcinilor reale ale unei ecuaţii algebrice.

Considerăm ecuaţia algebrică f(x) = 0 de gradul n şi formăm derivatele . Fie c un număr pozitiv pentru care toate polinoamele precedente sunt pozitive. Atunci c este margine superioară a rădăcinilor pozitive.

Secolul al XVIII-lea

În acest secol au apărut în cadrul teoriei numerelor ecuaţiile nedeterminate.

a) O ecuaţie nedeterminată în doua variabile de gradul întâi este de forma:

,

unde a, b, c sunt coeficienţi întregi, iar x, y sunt necunoscute, numere întregi. O astfel de ecuaţie este numită  ecuaţie diofantică, fiind considerată prima oară de către Diofant (sec. III-IV).

Condiţia necesară şi suficientă ca o ecuaţie diofantică să aibă soluţii este ca cel mai mare divizor comun al numerelor a şi b să fie divizor al lui c. Dacă (x0, y0) este soluţie particulară a ecuaţiei, atunci 

,

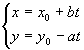t fiind un număr întreg arbitrar, este soluţia ecuaţiei.

Joseph Lagrange a dat în 1767 metoda obişnuită de obţinere a unei soluţii particulare (x0, y0) a ecuaţiei, prin dezvoltarea în fracţie continuă finită a numărului  raţional. Soluţia particulară care generează soluţia generală este:

b) Un interes deosebit a continuat să-l prezinte studiul ecuaţiei cuadrice principale:

în mulţimea numerelor naturale, deci excluzând soluţia banală x = 0, y= 1 şi presupunând ca a > 0 nu este pătrat perfect.

Ecuaţia menţionată a fost considerată prima dată de către Arhimede (sec. III î.e.n) şi studiată de către Diofant (sec. III-IV), Brahmagupta (sec. VII), Baskara (sec. XI), Fermat (sec. XVII); cercetată în continuare de către Leonhard Euler, Joseph Lagrange, Adrien Legendre.

Fermat a indicat o metodă de rezolvare, numită metoda cascadelor. În 1762, Euler a rezolvat ecuaţia prin dezvoltare în fracţie continuă a numărului . El a considerat şi ecuaţia în numere întregi 

pe care a readus-o la forma simplă

,

pe care a numit-o ecuaţie Pell.

În algebră, deşi ecuaţiile de gradul al treilea şi al patrulea erau rezolvate din secolul XVI de către Fontana şi Ferrari, au fost căutate şi în secolul al XVIII-lea noi mijloace de rezolvare, în speranţa că ele ar fi aplicabile şi ecuaţiilor de grad mai mare.

Leonhard Euler, în 1762, a redus ecuaţia 

la forma canonică

prin substituţia

,

z1, z2 fiind rădăcinile ecuaţiei rezolvente.

Relativ la teoria generală a ecuaţiilor, dupa ce s-a recunoscut că mulţimea numerelor complexe conţine ca un caz particular şi numerele reale s-a putut enunţa propoziţia fundamentală în teoria ecuaţiilor, anume: că orice ecuaţie cu coeficienţi reali sau complecsi admite rădăcină. Aceasta propoziţie este numită lema lui d'Alembert, deoarece Jean d'Alembert a enunţat-o şi a schiţat o soluţie, în 1746.

Leonhard Euler a afirmat că numărul de rădăcini ale unei ecuaţii algebrice este egal cu gradul ei.

Colin Maclaurin a observat, în 1792, că pentru o ecuaţie algebrică cu coeficienţi reali, rădăcinile complexe sunt în număr par.

Bezout a demonstrat în 1799 teorema fundamentală următoare: Un sistem de m ecuaţii în m necunoscute, de grade respectiv n1, n2, .., nm are n1n2..nm soluţii.

Referitor la metodele numerice de calcul, menţionăm regula lui Paolo Ruffini, din 1799, care dă succesiv zecimalele rădăcinii. Presupunem că o rădăcină a ecuaţiei f(x) = 0 este cuprinsă între întregii a şi a+1; substitutia y = x+a conduce la o ecuaţie g(x) = 0 cu o rădăcina între 0 şi 1. Substituind, pe rând, valorile 0,1; 0,2 ; pâna obţinem o variatie; fie aceasta între 0,b şi 0,b+0,1. O substituţie z=y+0, b conduce la o ecuaţie h(z) = 0 cu o rădăcină între 0 şi 0,1.

În cadrul analizei, ecuaţiile diferenţiale au fost considerate de la sfârşitul secolului al XVII-lea. Newton şi Leibniz au integrat ecuaţii de forma

Leibniz a integrat ecuaţiile cu variabile separabile; Jacob Bernoulli a integrat ecuaţia diferenţială lineară şi ecuaţia reductibila la ea, care-i poartă numele; Johann Bernoulli a integrat, în 1708, ecuaţia diferenţială omogenă şi a introdus metoda factorului integrant pentru ecuaţia diferenţială de primul ordin, în două variabile.

Jacopo Riccati a studiat ecuaţiile diferenţiale integrabile prin transformări algebrice; a studiat probleme relativ la curbura unor curbe plane, care conduc la ecuaţii de ordinul al doilea în două variabile.

Alexis Clairaut a exprimat, în 1740, proprietatea caracteristică a factorului integrant l (x,y) al expresiei diferenţiale pdx + qdy, anume 

.

Pentru o soluţie a acestei ecuaţii cu derivate parţiale, următoarea expresie devine o diferenţiala exactă:

.

Joseph Lagrange a introdus în 1775 metoda variaţiei constantelor pentru determinarea unei integrale particulare a ecuaţiei diferenţiale lineare, când cunoaştem integrala generală a ecuaţiei omogene.

Secolul al XIX-lea

Lucrările lui Lagrange şi Ruffini (sec. XVIII) au arătat că nu putem să rezolvam în radicali ecuaţiile de gradul cinci, în sus. Astfel Abel a arătat că, prin metoda lui Lagrange, putem să rezolvam în radicali ecuaţiile algebrice ale căror rădăcini formează un ciclu faţă de o operaţie raţională, q (x), adică rădăcinile sunt:

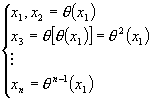
Astfel de ecuaţii sunt numite ecuaţii abeliene.

În 1821 Cauchy a elaborat un nou procedeu de interpolare, punându-şi problema următoare: să se determine o funcţie raţională în care numărătorul are un grad determinat n, numitorul un grad determinat m şi care să ia pentru m+n+1 valori arbitrare x0,x1,..,xm+n ale variabilei , m+n+1 valori u0, u1, .. ,um+n date arbitrar.

Joseph Liouville a dat o bază teoretică metodei iteraţiei pentru rezolvarea ecuaţiilor numerice de forma x = f(x), unde , care constă în următoarele etape succesive: în intervalul în care avem o singură rădăcina luăm o valoare x0 arbitrară; apoi formăm şirul x1 = f(x0), x2 = f(x1), .. , xn+1 = f(xn), .. care are o limită egală cu rădăcina însuşi. Luând x = xn, eroarea este .

În 1870 teoria lui Galois este aplicată sub forma data de Camille Jordan: Condiţia necesară şi suficientă pentru ca o ecuaţie să fie rezolubilă în radicali este ca factorii de compoziţie ai grupului Galois ataşat să fie toate numere prime. Otto Hölder a dovedit în 1889 că grupurile factor nu depind de considerarea succesiunii factorilor. Leopold Kronecker şi-a propus în 1853 să obţina toate ecuaţiile rezolubile în radicali, în afara celor determinate de Abel. El a recunoscut ca orice ecuaţie de grad prim p este abeliană, când cunoaştem un număr r care este rădăcina unei ecuaţii abeliene de grad p-1.

 

2. Lucrarea este structurată pe două capitole şi o bibliografie

Capitolul 1 are un caracter eterogen - la începutul acestuia se introduc notaţiile folosite pe parcursul lucrării şi noţiunile de bază. În continuare este definită teoria generală a metodelor iterative în cazul ecuaţiilor şi sistemelor neliniare.

Capitolul 2 are ca obiect rezolvarea ecuaţiilor şi sistemelor de ecuaţii neliniare cu ajutorul metodei lui Newton. Sunt examinate, în cele trei subcapitole, metoda lui Newton pe axa reală, metoda lui Newton în spaţiul Rn şi metoda lui Newton în spaţii Banach, împreună cu limbajul pseudocod utilizat pentru descrierea algoritmilor.