METODA LUI NEWTON

 2.1.Metoda lui Newton

 Metoda lui Newton sau metoda tangentei este o metoda aplicata în practica pentru rezolvarea ecuatiilor si sistemelor neliniare. Aceasta metoda este importanta deoarece cu ajutorul ei se pot trage concluzii privind existenta, unicitatea si domeniul în care se gaseste solutia fara a o gasi în mod explicit.

În continuare vom prezenta metoda lui Newton în spatiile R, Rⁿ si spatii Banach.

2.1.1Metoda lui Newton în spatiul R

 Metoda lui Newton în spatiul R este cunoscuta si sub numele de metoda tangentei.

Se considera functia f : [a,b] ® R de clasa C¹([a,b]).

Presupunem ca în intervalul [a,b] ecuatia f(x) = 0 admite o singura radacina x*.

În figura se poate urmari constructia sirului iterativ x_k.

Se alege ca punct de plecare punctul x₀ = b si în punctul M₀(x₀ , f(x₀)) se duce tangenta la graficul functiei care intersecteaza axa OX în punctul x₁. În continuare vom duce o tangenta în punctul M₁(x₁ , f(x₁)) care taie axa OX în punctul x₂ si asa mai departe pâna se formeaza sirul iterativ x_k.

Sirul x₀, x₁, … converge catre x* care este radacina ecuatiei f(x) = 0.

Presupunem ca am ajuns în punctul M_n(x_n , f(x_n)) si trebuie sa scriem ecuatia tangentei dusa la graficul functiei. Ecuatia tangentei arata astfel:

Pentru y = 0 rezulta x = x_n+1.

Înlocuind în ecuatie obtinem:

.

De unde rezulta:

.

Fie functia iterativa      . Deoarece j (x) este iterativa, atunci x_n+1 = j (x).

Trebuie asigurata existenta sirului iterativ ( f¢ (x_n) ¹ 0) si convergenta sirului catre x*.

 Teorema (OSTROWSKI)

Fie f Î C²([a,b]) si fie x₀ Î [a,b]. Presupunem ca urmatoarele conditii sunt îndeplinite:

1. f¢ (x₀) ¹ 0;

2. [x₀ , x₀+2h₀] = I₀, unde              este inclus în intervalul [a,b];

3.        , unde , x Î I₀.

Atunci ecuatia f(x) = 0 are o unica solutie x* Î I₀ , iar sirul {x_k}_{kÎ N} dat de metoda lui Newton este bine definit si converge la x*.

Eroarea aproximatiei este data de:

.

Dem:

Aplicam formula cresterilor finite pentru functia f¢ în punctele x₀ si x₁:

.

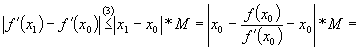
Folosind inegalitatea triunghiului obtinem:

De aici rezulta : si deci x₂ este bine definit.

Fie

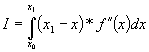
Calculam I în doua moduri:

1) Prin parti

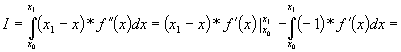
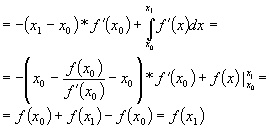
2) Se face schimbarea de variabila:

x = x₀ + h₀ * t;

dx = h₀ dt

(*)

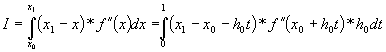Notam:

Pentru

Atunci, înlocuind în (*) obtinem:

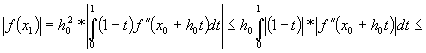
are sens pentru ca conditia 1) este evidenta.

Trecând pe h₁ în modul obtinem:

.

Vom arata ca:

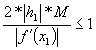
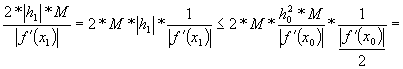
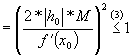
De aici rezulta:

.

Luam I₁ = [x₁ , x₁+2h₁]. Dorim sa aratam ca I₁ Ì I₀.

Pentru a demonstra ca I₁ Ì I₀ aratãm ca

.

.

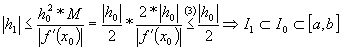Prin recurenta se obtine pentru orice numar natural kÎ N ca: f¢ (x_k) ¹ 0;

; ;

;

.

De aici rezulta ca sirul {x_k}_{kÎ N} este bine definit.

În continuare vom demonstra ca sirul {x_k}_{kÎ N} este un sir Cauchy.

este descrescator si lungimea intervalului tinde catre 0.

, de unde rezulta ca sirul este fundamental.

Orice sir fundamental este convergent, rezulta ca exista limita sirului {x_k}_{kÎ N} si se noteaza cu

.

.

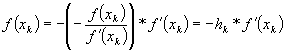Trecând la modul obtinem:

, unde

.

De aici rezulta ca f(x_k) ® 0.

Deoarece f este continua, rezulta ca:

, deci x* este solutie a ecuatiei f(x) = 0.

În continuare aratam ca solutia ecuatiei f(x) = 0 este solutie unica în [a,b].

Fie un punct x Î ( x₀ , x₀ + h₀ ).

Aplicam formula cresterilor finite pentru functia f¢ si obtinem:

Rezulta ca: Þ f monoton crescatoare f¢ (x)>0 sau f monoton descrescatoare f¢ (x)<0 pentru orice x Î ( x₀ , x₀ + h₀ ). Rezulta ca taie axa OX, dar într-un singur punct, deci am asigurat unicitatea solutiei.

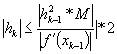
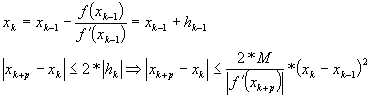
Facem ca p ® ¥ si obtinem pentru k fixat:

Def.: Sirul iterativ {x_k}_{kÎ N} convergent catre x* are ordinul de convergenta pÎ R daca: , unde c este o constanta si

este valoarea absoluta.

Deci:

.

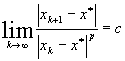Daca p=1, atunci spunem ca avem o convergenta liniara, iar pentru p=2 avem o convergenta patratica.

Daca 1 < p < 2, atunci avem convergensa superliniara.

Obs.: Cu cât p este mai mare cu atât sirul iterativ va fi mai rapid convergent.

Teorema

Sirul iterativ obtinut prin metoda tangentei are ordinul de convergenta patratica.

 Dem :

Conform formulei lui Taylor:

Stim ca       , atunci înlocuind în ecuatia de mai sus obtinem:

Împartind ecuatia cu ( x* -x_n )² obtinem:

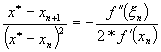
Trecând la limita obtinem:

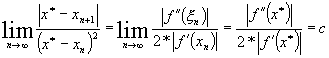
Folosind rezultatele din aceasta teorema se poate obtine si un alt criteriu de oprire.

, unde

Din inegalitatea de mai sus obtinem:

Pentru:

n = 0 avem:

n = 1 avem:

………………………………………

n

Impunem conditia ca c*D (x₀) < 1. Din aceasta conditie si ultima inegalitate rezulta:

De aici rezulta ca x_n+1 ® x*.

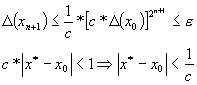
Avantajul metodei lui Newton este faptul e o metoda rapid convergenta.

Dezavantajul metodei lui Newton este faptul ca e o metoda locala, adica punctul initial de plecare x₀ trebuie sa fie suficient de aproape de radacina cautata x*.

Un alt dezavantaj al metodei este faptul ca necesita derivata de ordin I.

În practica derivata de ordin I se înlocuieste cu ajutorul formulelor de derivare numerica, adica:

, unde h este foarte mic, h > 0.

Ca sa calculam de fiecare data derivata functiei f în punctul x_n se foloseste metoda simplificata a lui Newton care arata astfel:

.

Alegerea punctului initial de plecare

Punctul initial de plecare se alege astfel:

Algorim metoda tangentei

Fie a, b, f, e e -precizie dinainte data

Fie y:=a;

Daca atunci y:=b;

Repeta

x:=y;

y:=j (x);

pâna când ;

Tipareste y;

2.1.2.Metoda lui Newton în spatiul Rⁿ

 Se considera functia f_I :D Í Rⁿ ® R, si sistemul f_I(x₁,…,x_n) = 0, si (x₁,…,x_n) Î D.

Daca se considera aplicatia f : D® Rⁿ, astfel încât:

, atunci sistemul poate fi scris si sub forma ecuatiei vectoriala: f(x) = 0, unde xÎ D si 0 este elementul nul al spatiului Rⁿ.

Se considera ecuatia f(x) = 0.

Fie x* Î D o solutie a acestei ecuatii, iar x^(k) o aproximatie a lui x*. Notând cu e ^(k) eroarea de aproximare a lui x* prin x^(k) avem:

x* = x^(k) + e ^(k).

Pentru n = 2 în spatiul R² avem un sistem neliniar:

, unde f, g : D Í R² ® R.

Consideram notatia: .

Consideram punctul de plecare (x₀ , y₀) în care ducem o dreapta perpendiculara pe planul XOY care intersecteaza suprafetele în punctele M₁ si M₂. Ducem doua plane tangente la cele doua suprafete în punctul M₁, respectiv M₂. Cele doua plane se intersecteaza dupa o dreapta care taie planul XOY în punctul (x₁ , y₁) care este urmatorul punct de iteratie.

Fie sistemul sub forma implicita:

  .

Presupunând ca am ajuns în punctul de iteratie (x_k , y_k) Î XOY calculam derivatele functiilor f si g:

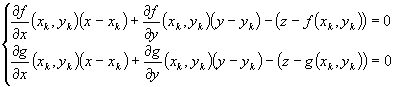
Din cele doua ecuatii scoatem pe z si obtinem urmatorul sistem de ecuatii:

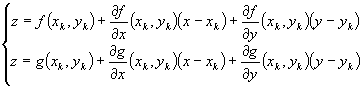
Pentru z = 0 obtinem urmãtorul punct de iteratie (x_k+1 , y_k+1) Î XOY si se formeaza urmatorul sistem:

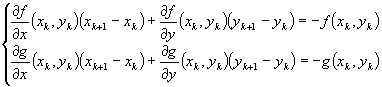
Rezolvam sistemul astfel:

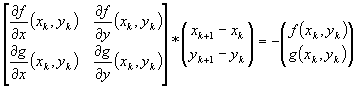
Scoatem pe x_k+1 si y_k+1 si obtinem:

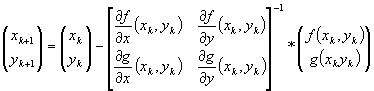
Notam cu 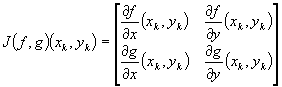, unde J(f,g)(x_k,y_k) reprezinta matricea jacobiana.

Astfel vom obtine:

x^k+1 = x^k – J^-1(x_k) * f(x_k), adica

x^k+1 = x^k – (f¢ (x_k))^-1 * f(x_k).

Fie f : Rⁿ ® Rⁿ unde f = (f₁ ,…,f_n )

Pentru obtinerea solutiei x a sistemului vom dezvolta aceasta functie în serie Taylor în vecinatatea unui punct x_k:

Îi atribuim lui x valoarea x_k+1 si obtinem:

  , de unde

.

Fie sistemul f(x) = O _Rⁿ .

 Teorema (Kantorovici)

Fie functia f : D Ì Rⁿ ® Rⁿ o functie data, diferentiabila Frechet pe o multime convexa D₀ Ì D si fie x⁰ Î D₀ punct initial de plecare.

Presupunem ca urmatoarele afirmatii sunt satisfacute:

1. Exista (f¢ (x⁰))^-1 si

;

2.

, " x,y Î D₀.

3.

4.

5. B₀ = B(x⁰,r₀) Ì D₀, unde                                      ;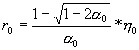

atunci ecuatia f(x) = O _Rⁿ admite o unica solutie x* Î D₀, iar sirul {x_k}_{kÎ N} dat de metoda lui Newton-Raphson este bine definit si converge la solutia ecuatiei x*.

Eroarea la iteratia k este data de:

Pregatirea demonstratiei

Fie X,Y doua spatii normate reale peste un spatiu K.

Notam cu L(X,Y) = {T : X® Y ½ T liniara} – multimea tuturor operatorilor liniari.

Lema1

Spatiul L(X,Y) este o algebra.

Dem:

, " xÎ X , " T,S Î L(X,Y);

, " x Î X , " a Î R , " T Î L(X,Y);

, " x Î X , " T, S Î L(X,Y).

L(X,Y) satisface axiomele unei algebre cu operatiile definite mai sus, adica: (L(X,Y) , + , *) formeaza un spatiu vectorial real si (L(X,Y) , + , ° ) formeaza un inel.

Def.

Fie T:X® Y un operator liniar. Spunem ca T este marginit daca exista o constanta pozitiva c astfel încât:

, " x Î X.

Lema2

Fie T:X® Y un operator liniar. Atunci T este continuu daca si numai daca T este marginit.

Notam:

Lema3

(L(X,Y) , ) este o algebra normata notata cu L(X,Y).

Dem.:

Avem de verificat conditiile:

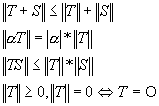
Lema4

Daca TÎ L(X,X) astfel încât , unde I este un operator unitate, atunci T este un element inversabil în algebra si

.

Dem.:

Fie sirul . Vom arata ca acest sir este un sir Cauchy în spatiul L(X,X).

Fie N > M, atunci:

.

Dar spatiul L(X,X) este un spatiu complet, deci exista limita:

Î L(X,X) .

Din compunerea celor doua spatii obtinem:

De aici rezulta ca:

.

Calculam norma lui T^-1 si obtinem:

.

Lema5

Daca T,S Î L(X) astfel încât exista T^-1Î L(X) si si a *b <1, atunci exista S^-1Î L(X) si                                                     .

Dem.:

Fie

.

Deoarece:

, conform lemei4 rezulta ca I_x –U este inversabil în spatiul L(X) si

Deci exista inversul lui S.

Deoarece:

.

Calculam norma lui S^-1 si obsinem ceea ce trebuia demonstrat:

.

Rezultatele anterioare se pot particulariza prin alegerea lui X=Rⁿ. Se va obtine ca spatiul L(Rⁿ), spatiul matricilor de ordin n, este o algebra Banach în care sunt valabile lemele 4 si 5.

 Lema6

Fie G: DÌ Rⁿ ® Rⁿ un operator diferentiabil Frechet pe o multime convexa D₀ Ì D. Presupunem ca derivata Frechet G¢ are proprietatea Lipschitz pe D₀:

, " x,y Î D₀.

Atunci pentru orice x, y Î D₀ avem:

.

 Demonstratia teoremei Newton-Raphson-Kantorovici

 Se observa conform conditiei 3 ca:

Întrucât h ₀ < r₀ , rezulta ca x¹ Î B₀.

Asadar, putem folosi conditiile 2 si 4 si avem:

.

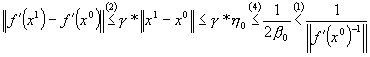Conform lemei5 exista ( f¢ (x¹))^-1 si

,

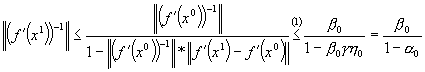unde :

Definim:

.

Deci, urmatoarea iteratie x¹ satisface o relatie de forma (1).

Vom cauta sa aratam ca sunt satisfacute relatiile analoage si (3), (4), (5).

Se observa ca pentru T= ( f¢ (x⁰))^-1 * f¢ (x¹) avem:

Conform lemei4 exista T^-1 si

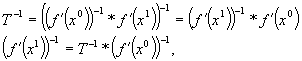
Adica, vom avea

.

Trecând la norma obtinem:

.

Pentru a majora pe se introduce operatorul : G(x)=x-(f¢ (x⁰))^-1f(x), unde G este diferentiabil Frechet pe domeniul D₀ si diferentiala                    .

Deci, vom avea:

.

Notam G¢ (x⁰) = O _n.

Conform lemei6 avem:

.

Daca notam obtinem o relatie analoaga cu conditia 3, adica:

Notând                                          obtinem:

.

Consideram sfera B₁ = B(x¹,r₁), unde 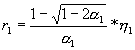. Înlocuind pe a ₁, h ₁ cu expresiile lor

în functie de a ₀, h ₀, obtinem prin calcul direct:

r₁ = r₀ - h ₀.

Aratam ca B₁ Ì B₀.

Fie xÎ B₁, deci . Prin urmare:

, adica x Î B₀ si B₁ Ì B₀.

Prin inductie matematica (trecerea de la k la k+1 este absolut similara cu trecerea de la 0 la 1 ) se poate arata ca pentru orice k Î N exista

si

, unde:

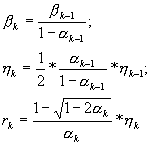
Din aceste relatii rezulta ca sirul (x^k)_k dat de metoda lui Newton este bine definit si apartine lui B₀.

Pentru convergenta sirului observam ca:

.

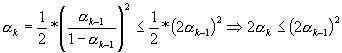Se itereaza si obtinem:

Prin urmare: .

Pe de alta parte:

, de unde rezulta ca .

Prin calcul direct obtinem ca  , deci (B_k) este un sir descendent de multimi cu diametrul tinzând la zero. Conform teormei lui Cantor exista un singur punct x* care apartine la toate multimile B_k, iar sirul (x_k) (centrele sferelor) converge la x*.

Pentru a arata ca x* este solutia ecuatiei f(x) = O _Rⁿ se observa ca functionala este continua pe B₀ , f¢ fiind lipschitz.

Deci, este marginit pe B₀ conform teoremei lui Weiersstras, deci   , " x Î B₀.

.

De aici rezulta ca:

.

Pentru evaluarea erorii avem:

.

 Algoritm metoda Newton-Raphson-Kantorovici

-date de intrare: f, e, y(=x⁰).

repeta

x:=y;

y:=j (x);

pâna când                    

tipareste y;

 2.1.3.Metoda lui Newton în spatii Banach

 2.1.3.1.Ecuatii de tip P(x) = 0

 1.Fie operatorul P care aplica multimea deschisa W din spatiul Banach X în spatiul Banach Y: P:W Ì X ® Y.

Presupunem ca în multimea W exista un element x* astfel încât P(x* ) = 0. Fie x₀ Î W. Presupunem ca operatoul P are o derivata continua în L; putem înlocui elementul P(x₀) = P(x₀) – P(x* ) cu expresia P¢ (x₀)(x₀-x* ) si, în consecinta, solutia ecuatiei P¢ (x₀)(x₀ - x) = P(x₀) sa fie apropiata de x*.

Aceasta ecuatie este liniara, iar solutia ei este:

.

Pornind de la aproximatia initiala x₀, continuând acest proces obtinem un sir (x_n)_n definit prin:

.

Fiecare x_n este o solutie aproximativa a ecuatiei P(x) = 0, cu atât mai precisa cu cât n este mai mare.

Aceasta metoda care duce la construirea sirului (x_n)_n se numeste metoda lui Newton.

 2.Fie ecuatia:

x = S(x), (1)

unde operatorul S este definit pe bila din spatiul Banach X, x_0Î X.

Consideram si ecuatia reala:

t = j (t), (2)

unde functia j este definita pe intervalul [t₀ , t¢ ].

Spunem ca functia j (ecuatia (2)) majoreaza operatorul S (ecuatia (1)) daca:

1)

2)

;pentru

     (3)

 Teorema1

Fie operatorul S având derivata continua în bila închisa W ₀ ( ), iar functia j diferentiabila pe [ t₀ , t¢ ]. Atunci, daca ecuatia (2) majoreaza ecuatia (1), iar ecuatia (2) are o radacina în intervalul [ t₀ , t¢ ], ecuatia (1) va avea si ea o solutie x* catre care converge sirul (x_n)_n:

x_n+1 = S(x_n) , n = 0, 1, … ,

având ca punct initial x₀.

În acest caz:

,

unde t* este cea mai mica radacina din intervalul [t₀ , t¢ ] a ecuatiei (2).

 Dem.:

Pentru început aratam ca sirul aproximatiilor succesive pentru ecuatia (2): t_n+1 = j (t_n) este convergent.

Astfel, din conditia 2) rezulta inegalitatea j ¢ (t)³ 0, tÎ [t₀ ,t¢ ], deci functia j este crescatoare pe intervalul [ t₀ , t¢ ]. De aici rezulta ca t_n are sens pentru orice n si în plus:

este radacina ecuatiei (2), a carei existensa este asigurata din ipoteza.

Pentru n = 0 aceasta inegalitate este certa si daca ea are loc si pentru n = k din rezulta ca , adica , atunci conform monotoniei functiei j si prin inductie ea are loc pentru orice n.

Din rezulta ca , iar inegalitatea este consecinta ipotezei 1). Astfel, am demonstrat existenta limitei care conform continuitatii functiei j rezulta ca t* este radacina a ecuatiei (2) si este cea mai mica radacina di intervalul [ t₀ , t¢ ].

Aratam ca toate elementele x_n+1 = S(x_n) au sens si formeaza un sir convergent.

Reprezentând ecuatia (3) sub forma:

, observam ca x₁ Î W ₀.

Presupem ca x₁,x₂,…x_{nÎ W 0} si ca:

. Atunci avem:

.

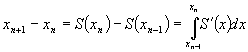Notam prin x si t punctele corespunzatoare intervalelor [x_n-1, x_n] si [t_n-1, t_n], atunci:

.

Atunci vom avea:

.

În conformitate cu conditia 2) avem: si obtinem:

  .

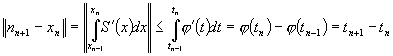Am aratat ca x_n+1 Î W ₀, deoarece:

Deci, am demonstrat ca prin inductie ca x_k Î W ₀, pentru orice k = 0, 1, …

Deoarece:

,

sirul (x_n)_n este fundamental, deci are limita.

Notam cu .

Trecând în ecuatia x_n+1 = S(x_n) la limita si tinând cont de continuitatea operatorului S obtinem:

x* = S(x* ), adica x* este radacina a ecuatiei (1).

Estimarea rezulta din . Dacã punem n = 0 obtinem:

.

Trecând la limita pentru p® ¥ obtinem:

.

Observatii

1. Inegalitatea ne da o estimare a vitezei de convergenta a sirului (x_n)_n catre x*.

2. Ecuatia (1) poate avea în bila W ₀ si alte radacini diferite de x*, chiar daca solutia t* este unica în intervalul [t₀ ,t¢ ]

 3.Investigarea metodei lui Newton pentru ecuatia P(x) = 0.

Fie operatorul P definit pe bila W ( )din spatiul X si are bila închisa W ₀ () derivata a doua continua.

Consideram ecuatia reala: y (t) = 0.

Presupunem ca functia j este de doua ori continuu diferentiabila pe intervalul [t₀ ,t¢ ], unde t¢ = t₀ +r .

Teorema2

Fie urmatoarele conditii îndeplinite:

1) exista operatorul liniar continuu

;

2)

;

3)

;

4)

, pentru

5) ecuatia are în intervalul [t₀ , t¢ ] radacina .

Atunci metoda lui Newton luând ca aproximatii initiale x₀ si t₀ converge catre solutiile x* si t*, iar

.

Dem.:

Metoda lui Newton pentru ecuatia P(x) = 0 este echivalenta cu metoda aproximatiilor succesive aplicata ecuatiei x = S(x), unde

În acelasi timp putem înlocui aplicarea algoritmului lui Newton modificat ecuatiei y (t) = 0 cu aproximatiile succesive pentru ecuatia t = j (t), unde:

.

Aratam ca pentru aceste ecuatii sunt satisfacute ipotezele teoremei 1.

Avem:

Conform conditiei 3) avem:

.

Folosind reguluile de diferentiere, obtinem:

si atunci:

.

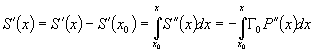Folosind conditia 4) avem:

;

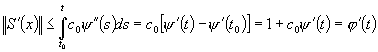daca x si t satisfac inegalitatea                             .

 Teorema3

Fie îndeplinite conditiile teoremei2. Atunci algoritmul lui Newton pentru ecuatia P(x) = 0, având ca punct initial x₀, este realizabil si conduce la sirul (x_n)_n care converge catre radacina x* a ecuatiei P(x) = 0.

Dem.:

Din teorema 2 rezulta ca x₁ are sens si x₁ Î W ₀.

Verificam daca ipotezele teoremei 2 ramân valabile daca înlocuim x₀ cu x₁, iar t₀ cu t₁. Consideram operatorul:

.

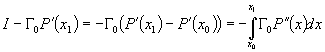Normând obtinem:

.

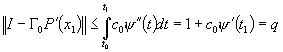Având în vedere ca pe tot intervalul [t₀ , t¢ ], iar , minimul functiei y (t) nu poate fi atins la stânga punctului t*. Deoarece t₁ £ t* si    rezulta ca:   si deci q < 1.

În conformitate cu teorema lui Newton exista operatorul liniar continuu:

, cu proprietatea ca:

, unde                                          .

În consecinta exista operatorul liniar continuu:

.

Deci, conditiile 1) si 2) sunt verificate.

În continuare demonstram ca:

.

Conform formulei lui Taylor avem:

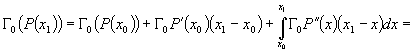
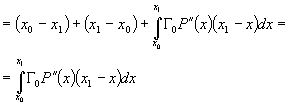
Procedând în mod analog obtinem:

.

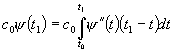Deoarece pentru punctele corespunzatoare x si t din segmentele [x₀ , x₁] si [t₀,t₁] avem:

, obtinem:

.

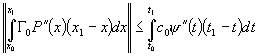Tinând seama de relatiile (4) si (3) obtinem:

  , deci ipoteza 3) este satisfacuta.

Conditia 4) se verifica asemanator.

Se observa ca daca:          , atunci                   . De aceea:

.

Conditia 5) nu este încalcata, deoarece daca radacina apartine intervalului [t* ,t¢ ], ea va apartine si intervalului [t₁ , t¢ ].

Deoarece sirul (t_n)_n este crescator si marginit, el va avea limita , iar din inegalitatea:

, rezulta ca sirul (x_n)_n are limita .

Din (1) obtinem relatia:

.

Fie x Î W ₀, arbitrar. Folosind formula cresterilor finite avem:

, de unde rezulta ca sunt egal marginite.

Daca trecem la limita obtinem: , adica este radacina a ecuatiei (2)

Analog, este radacina ecuatiei y (t) = 0 si stiind ca , iar t* este cea mai mica radacina, atunci                                             .

Deoarece , atunci .

 4.Teorema lui Newton-Kantorovici

Fie operatorul P definit pe W si având derivata a doua continua în W ₀. În plus:

1) exista operatorul liniar continuu

;

2)

;

3)

.

Atunci, daca: (4) si , (5) atunci ecuatia P(x) = q _x are solutia x* catre

care converg algoritmii lui Newton (de baza si modificat). În acest caz:

.

Daca, în plus, pentru

avem:

, (6) iar pentru

avem:

, (7) atunci solutia x* este unica în bila W ₀.

Viteza de convergenta a algoritmului lui Newton este caracterizata de inegalitatea:

, (8) iar cea a algoritmului modificat, pentru

, de:

.(9)

Dem.:

Consideram functia reala y definita pe intervalul [0,r] astfel:

.

Verificam ca operatorul P si functia y satisfac toate ipotezele teoremei2. Valabilitatea conditiilor 1) - 4) este evidenta. Deoarece radacinile ecuatiei y (t)=0 sunt:

si

,

inegalitatea (4) ne asigura existenta radacinilor, iar conditia (5) ne garanteaza ca cea mai mica radacina r₀ este continuta în intervalul [0,r].

Pentru a demonstra inegalitatile (8) si (9) , care caracterizeaza viteza de convergenta, este suficient sa consideram doar sirurile reale (t_n)_n si (t¢ _n)_n de aproximatii succesive ale algoritmului lui Newton si, respectiv, a celui modificat.

Consideram, mai întâi, metoda de baza.

Notam:

,

,

,

.

Exprimam pe h_n, k_n, h_n prin aceleasi marimi, dar cu indexul mai mic cu o unitate. Observam ca:

Aplicând formula lui Taylor polinomului de gradul doi, vom obtine:

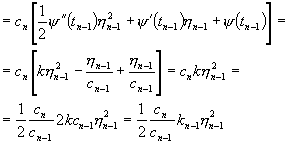
 Dar

(10)

Deci:

. (11)

Procedând similar, cu ajutorul relatiei (10), vom obtine:

.

De aici, obtinem:

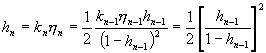. (12)

Din relatiile (11) si (12) obtinem, tinând seama de

,

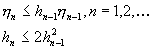
Deci, în consecinta,

si

.

De aici obtinem:

Rezulta estimarea relatiei (8).

Estimam, acum, eroarea metodei modificate.

Presupunem . Notând functia cu j putem scrie:

, unde

.

Dar , astfel ca:

.

De aceea:

În continuare, procedând la fel estimam s.a.m.d, obtinând în final:

.

 În final obtinem:

.

Observatie

1. Conditiile 2) si 3) ale teoremei pot fi înlocuite cu:

1¢ )

;

2¢ )

;

3¢ )

.

În acest caz h, r₀ si r₁ sunt date de:

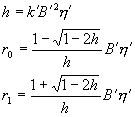
2. Relatiile (4), (5), (6) sunt precise, în sensul ca pentru ecuatia patratica y (t) = 0 încalcarea uneia dintre pimele doua relatii conduce la absebta solutiei acestei ecuatii, iar fara relatia (6) sau (7) nu avem unicitate.